분할 정복 알고리즘: 합병 정렬(Merge sort)와 퀵 정렬(Quick sort)

분할정복(Divide-and-Conquer) 알고리즘이란 주어진 문제의 입력을 분할하여 문제를 해결(정복)하는 방식의 알고리즘이다. 분할된 입력에 대하여 동일한 알고리즘을 적용하여 해를 계산하며, 이들의 해를 취합하여 원래의 문제의 해를 얻는다.
여기서 분할된 입력에 대한 문제를 부분문제(subproblem)라고 하고, 부분문제의 해를 부분해라고 한다. 부분문제는 더 이상 분할될 수 없을 때까지 분할해야 한다.
여기서 입력의 크기를 n이라고 했을 때 처음 주어진 문제가 2개의 부분문제로 분할되고, 각각의 입력 크기는 반 (n/2)가 된다. 또 한 번 분할하면 입력의 크기는 n/2² (n/4)가 된다. 계속해서 입력의 크기가 반씩 줄어들어 1이 되어 더 이상 분할할 수 없게 된다.

입력 크기가 n일 때 총 몇 번 분할해야 1이 될까?
분할한 총 횟수를 k라고 하자. 입력 크기는 분할할 때마다 2배로 작아지고 있다. 즉, k번 분할 후의 입력 크기는 n을 2의 k승으로 나눈 값이 된다.
따라서, 입력 크기가 n/2ⁱ = 1(지수로 쓸 수 있는 문자가 i밖에 없어서 이렇게 씁니다. 원래는 k일 때 더 이상 분할할 수 없으므로, k = log₂n임을 알 수 있다.
합병 정렬
합병 정렬은 입력이 2개의 부분문제로 분할되고, 부분문제의 크기가 1/2로 감소하는 분할 정복 알고리즘이다. 즉, n개의 숫자들을 n/2개씩 2개의 부분문제로 분할하고 각각의 부분문제를 순환적으로 합병 정렬한 후, 2개의 정렬된 부분을 합병하여 정렬한다.
합병이란 2개의 각각 정렬된 숫자들을 1개의 정렬된 숫자들로 합치는 것이다.
다음은 원소들이 각각 정렬되어 있는 배열 A와 B가 합병되어 정렬 C가 되는 것을 보여준다.

알고리즘
MergeSort(A,p,q) //A: 배열, p: 시작 인덱스, q: 끝 인덱스
입력: A[p] ~ A[q]
출력: 정렬된 A[p] ~ A[q]
if(p < q){ // 즉, A에 숫자가 2개 이상 있을 경우
k = (p+q)/2 // p+q가 홀수라 소숫점이 나온다면 k는 소슷점 이하를 버려준다
MergeSort(A,p,k) //재귀적으로 k가 1이 될 때까지 반복 (다만 처음과 끝의 인덱스가 달라짐)
MergeSort(A,k+1,q) //여기까지가 분할 알고리즘
A[p]~A[k]와 A[k+1]~A[q]를 합병한다.
}
분할은 크기를 1/2로 줄여나가는 것이기 때문에 쉽지만, 합병하는 것이 조금 어렵게 느껴질 수도 있다.
합병 알고리즘을 자세히 살펴보자
1.
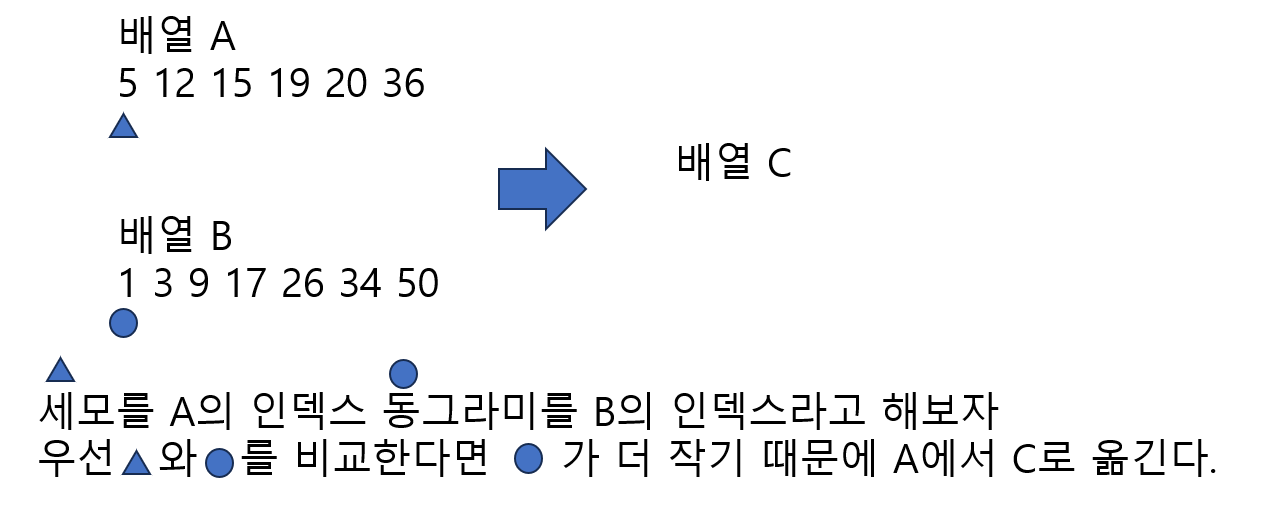
2.

3.

시간 복잡도
합병의 수행 시간은 합병되는 입력 크기에 비례하므로 각 층에서 수행된 비교 횟수는 O(n)이다.


| 입력크기 | 예 | 층 |
| n | 4 | |
| n/2 | 2 | 1층 |
| n/2² | 1 | 2층 |
위의 그림과 표를 살펴보면 합병의 수행시간은 합병되는 입력 크기에 비례하므로 각 층에서 수행된 비교 횟수는
O(n)이다. 그리고 층 수는 logn이다. (여기서는 log4 = 2)
즉, 합병 정렬의 시간 복잡도는 층수 x O(n) = O(n log n)이다.
하지만 합병 정렬에서 치명적인 단점이 있다. 두 개의 배열을 합병하기 위해 여분의 공간 C가 필요하다는 것이다.
컴퓨터 저장공간에 여유가 없다면 알고리즘을 실행하지 못할 수 있기 때문에 실용적이지 못하다.
퀵 정렬
퀵 정렬은 pivot이라는 배열의 원소(숫자)를 기준으로 pivot 보다 작은 숫자는 왼쪽으로, 큰 숫자는 오른쪽으로 위치하도록 분할하고, pivot을 그 사이에 놓는 것이다. 또 분할된 부분문제들에 대하여서도 위와 같은 과정을 순환적으로 수행하여 정렬한다.

알고리즘
QucikSort(A, left, right)
입력: A[left] ~ A[right]
출력: 정렬된 A[left] ~ A[right]
if(left < right){ // 원소가 2개 이상
pivot보다 작은 숫자들은 A[left]~A[p-1]로 옮기고, //p는 피봇 위치를 말함
큰 숫자는 A[p+1]~A[right]로 옮긴다. pivot은 A[p]에 놓는다.
QuickSort(A, left, p-1) //pivot보다 작은 그룹
QuickSort(A, p+1, right) //pivot보다 큰 그룹
}
시간 복잡도
퀵 정렬의 성능은 pivot 선택이 좌우한다. pivot으로 가장 작은 숫자 또는 가장 큰 숫자가 선택되면 시간 복잡도는 O(n²)이 된다.

- pivot이 3일 때: [6, 11, 9, 12]와 한 번씩 비교 -> 4회
- pivot이 6일 때: [11, 9, 12]와 한 번씩 비교 -> 3회
- pivot이 9일 때: [9, 12]와 한 번씩 비교 -> 2회
- pivot이 11일 때: [12]와 한 번씩 비교 -> 1회
총 비교 횟수는 4 + 3 + 2 +1 = 10
만일 입력의 크기가 n이라면, 퀵 정렬의 최악의 경우 시간 복잡도는 O(n²) 이다.
최선의 경우는 항상 1/2씩 분할한다면 최선의 경우가 될 것이다. (앞에서 살펴본 병합 정렬의 분할과 같음)
그럼 각 층에서 각각의 원소가 각 부분의 pivot과 1회씩 비교된다. 따라서 비교 횟수는 O(n)이다.
그러므로 총 비교 횟수는 O(n) x 층수 = O(n) x log n = O(n log n)이다. (병합 정렬과 같음)
pivot 선정 방법
퀵 정렬의 불균형한 분할을 완화시키기 위해서 일반적으로 다음과 같은 방법을 사용한다.
1. 랜덤 하게 선정하는 방법 (난수를 발생시켜 랜덤 한 숫자를 pivot으로 선택)
2. 3 숫자의 중앙값으로 선정하는 방법(Median of Three): 가장 왼쪽, 중간, 가장 오른쪽 숫자 중에서 중앙값으로 pivot을 정한다. 그럼 최악의 경우를 피할 수 있다.
